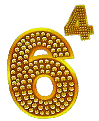Hatvány-azonosságok

 
Ha egy számot egyszer-sokszor
önmagával megszorzunk,
munkánk eredményeképpen
mindig egy hatványt kapunk.

Például nézzük csak ezt meg:
hatszor-hatszor-hatszor hat,
így írható egyszerűbben:
negyediken van a hat.

Hatványunknak az alapja
példánk szerint a hatos.
Kitevő lesz itt a négyes;
felső indexben lakos.

Persze olykor néhány hatvány
találkozik egymással,
ezért kell megismerkednünk
egy-két azonossággal.

Segítő szabályok ezek,
könnyebb velük számolni,
mint a saját fejünk után
össze-vissza szorozni.

Ha a hatványok alapja
egymással megegyező,
a szorzatuk szintén hatvány,
- talán nem is meglepő.

Eme hatvány kitevőjét
egyszerűen úgy kapjuk,
hogy a szorzat kitevőit
egymással összeadjuk.

Megegyező alapokkal
hatványokat úgy osztunk,
hogy a fenti kitevőből
az alsóét kivonjuk.

Amit kapunk szintén hatvány,
- mert mi más is lehetne?
Segít nekünk e két szabály,
s osztunk-szorzunk nevetve.

Ha szorzatot hatványozunk,
lehetőleg úgy tegyük,
hogy mindegyik tényezőjét
a hatványra emeljük!

És ha törtet hatványozunk,
ne cifrázzuk azt se túl!
Legyen hatvány, kitevővel,
épp úgy fölül, mint alul!

Hatvány lesz így az osztandó
és hatvány az osztott szám,
kitevője mindkettőnek
ugyanaz lesz. - Úgy biz’ ám!

Ha meg hatványt hatványoznánk,
változatlan alapra
kerüljön az eredeti
kitevőknek szorzata!

A hatvány-azonosságok
oda-vissza igazak,
de fordítva nem mondom el,
- logikázd ki te magad!